Rechnen

Potenzfunktionen mit ganzzahligem Exponenten

Beitragsautor Von admin
Beitragsdatum Januar 7, 2021

Lineare Funktion (Gerade)

$f(x) = mx+b$

m ist die Steigung, d.h. der Wert, um den 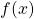$f(x)$ steigt, wenn x um eins größer wird und
b ist der y-Achenabschnitt, also der Wert, den 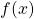$f(x)$ an der Stelle 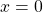$x=0$ annimmt, also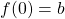 $f(0)=b$

Beispiel:

$f(x) = 2x+3$

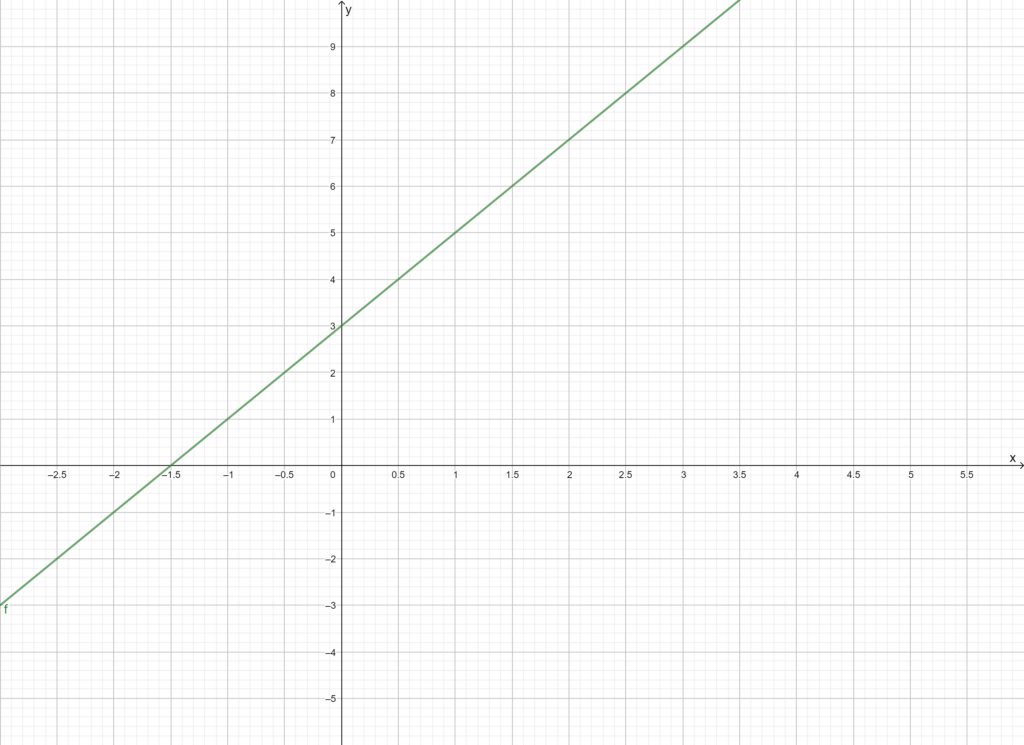
Um die Nullstelle x₀ einer Funktion zu ermitteln, muss die Funktion gleich Null gesetzt werden:

$0=f(x_0)$

$0=2x_0 + 3 | -3$

$-3=2 x_0 | :2$

$x_0 = -\frac{3}{2}$

Quadratische Funktion (Parabel)

$f(x) = ax^2+bx +c$

Die Parameter a, b, c nennt man die Koeffizienten der Potenzen

$x^2 , x^1 = x, x^0 = 1$

Beispiel:

$f(x) = 2x^2 - 12 x + 16$

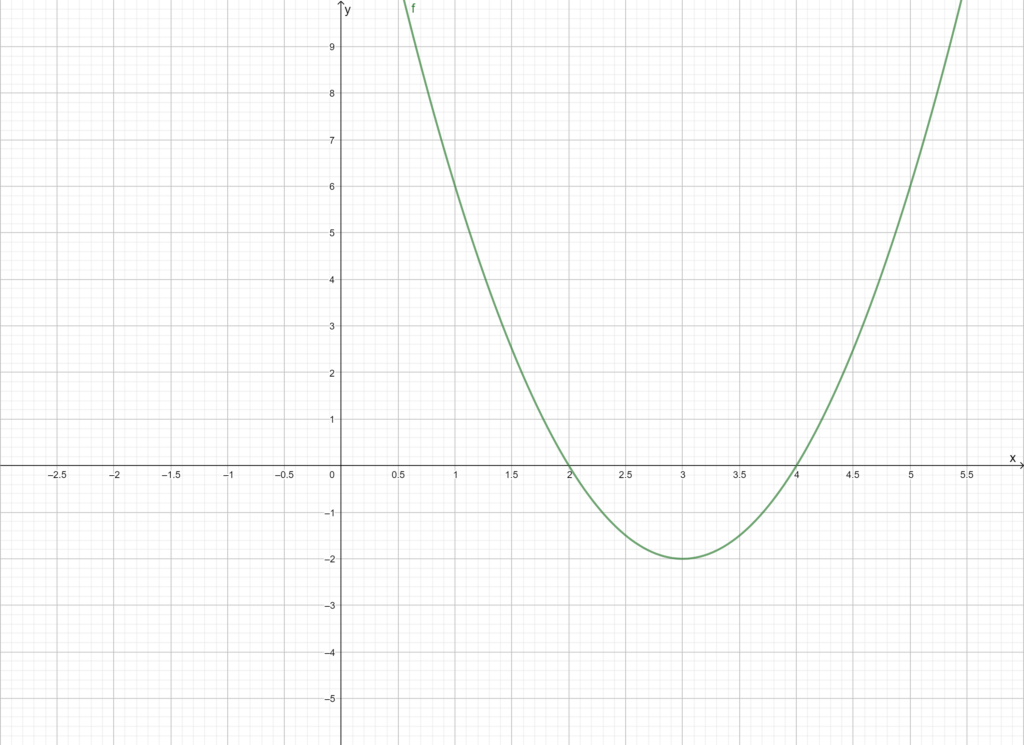
Den Schnittpunkt mit der y-Achse liest man direkt ab, denn

$f(0) = 16$

Rechnung erfordert die Ermittlung der Nullstellen, von denen es 2, 1 oder 0 geben kann, je nachdem wie der Graph liegt und die Berechnung des Extremums, das je nach Orientung des Graphens ein Minimum oder Maximum ist.

Die Ermittlung der Nullstellen erfolgt in 3 Schritten:

Gleich Null setzen

$0 = 2x^2 - 12 x + 16$

Den Faktor vor dem x² -Term ausklammern

$0 = 2 (x^2 - 6x + 8) | : 2$

p/q-Formel anwenden für

$0 = x^2 - 6x + 8$

p/q-Formel

$0 = x^2 + p x + q$

$x = -\frac{p}{2} \pm \sqrt{(\frac{p}{2})^2 - q}$

Also sind: p=-6 und q= 8

$x = 3 \pm \sqrt{9-8}$

Die Nullstellen sind daher:

$x_1 = 4, x_2 = 2$

Die Extremstelle ist das arithmetische Mittel der Nullstellen

$x_E = \frac{2+4}{2}=3$

Da der Parameter des x² -Terms $>0$ ist, ist die Parabel nach oben geöffnet und der Extremwert ist ein Minimum.
Den Funktionswert des Minimums erhält man durch Einsetzen der Extremstelle x_E = 3:

$f(x_E) = 2x_E^2 - 12 x_E + 16 |x_E=3$

$f(3) = 2 *3^2 - 12 *3 + 16$

$f(3) = -2$

Das Minimum ist also

$S=(3|-2)$

Mit diesen Werten kann man die Parabel in die Scheitelpunktform bringen:

$f(x) = 2 (x-3)^2-2$

Und nur mit dem Wissen der Nullstellen kann man die Parabel in die Produktdarstellung bringen, aus der sich die Nullstellen 2 und 4 direkt ablesen lassen.

$f(x) = 2 (x-2)(x-4)$