Kategorie: Rechnen

Exponential- und Logarithmusfunktion

Beitragsautor Von admin
Beitragsdatum Januar 16, 2021

Wenn eine zeitabhängige Größe G
mit Anfangsbestand B
während der Zeit t
in gleichen Zeitintervallen T
um den gleichen (Wachstums-)Faktor a größer wird,

dann wächst diese Größe G = G(t) in der Zeit t exponentiell:

$G(t) = B * a^{\frac{t}{T}$

Die Formel drückt sowohl exponentielles Wachstum als auch exponentiellen Zerfall aus.

0<a<1:	exponentieller Zerfall
a>1:	exponentielles Wachstum

Wenn sich beispielsweise ein Anfangbestand von zwei alle sechs Tage verdreifacht, dann hat man folgende Parameter:

Anfangsbestand B=G(0) = 2
Zeitintervallen T = 6 Tage
Wachstumsfaktor a = 3

$G(t) = 2 * 3^{\frac{t}{6}$

wobei die Zeit t in Tagen gemessen wird.

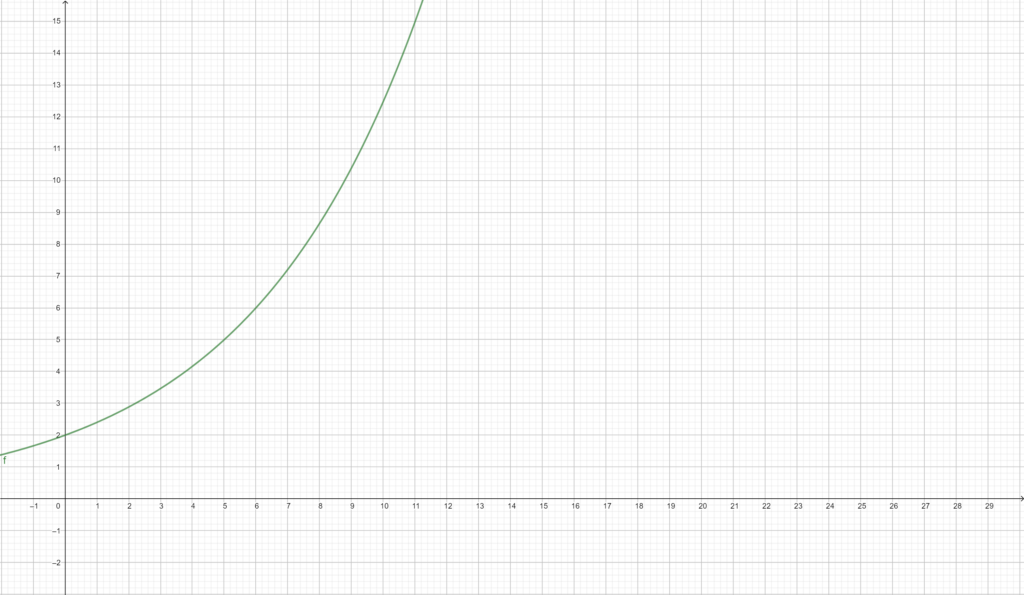
Aufgabe: Wie groß ist G nach 30 Tagen?

Lösung: Man setze t=30 ein und erhält G(30) = 486 Tage:

$G(30) = 2 * 3^{\frac{30}{6}} = 486$

Aber wie rechnet man, wenn die Aufgabe lautet: Nach wie vielen Tage ist G = 162?

Dann braucht man zur Lösung die Umkehrfunktion zur Exponentialfunktion.
Diese Funktion heißt Logarithmus zur Basis a: $log_a(x)$
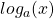
Umkehrfunktion heißt, wenn man diese in das Funktionsargument x einsetzt ergibt das wieder x:

$log_a(a^x) = x$

$a^{log_a(x)}=x$

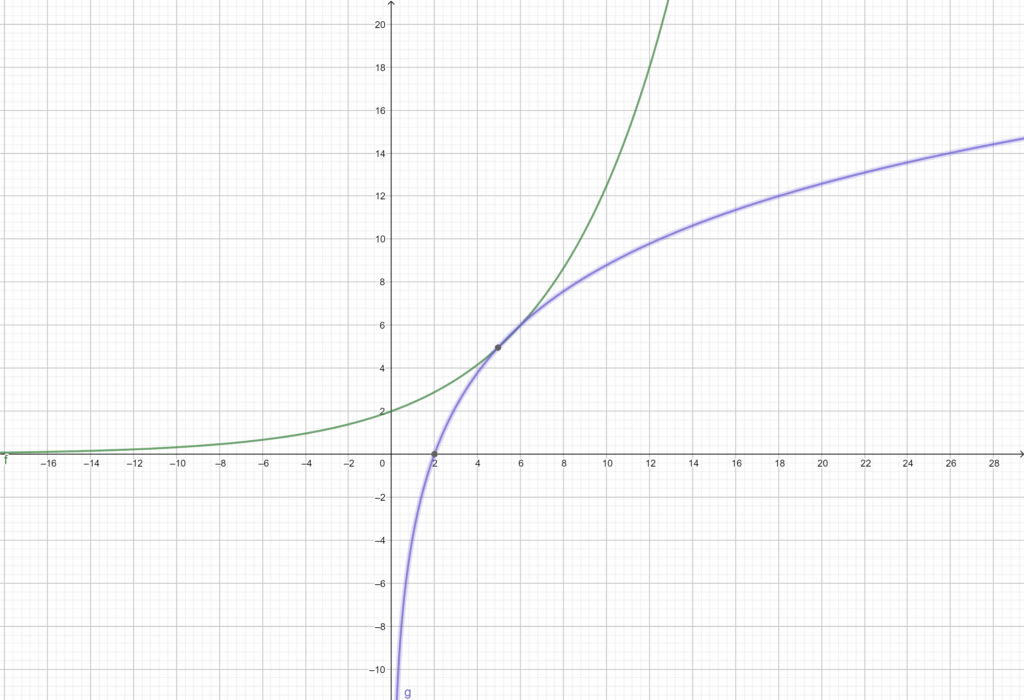
Das ist das Wesen der Umkehrfunktion. Grafisch dargestellt ergibt sich diese als an der Winkelhalbierenden gespiegelte Funktion.

Beispielsweise ist auch die Wurzelfunktion die Umkehrfunktion zur quadratischen Funktion:

$\sqrt{x^2}=x$

${\sqrt{x}}^2=x$

Dies wird sofort klar, wenn man sich daran erinnert, dass gilt:

$\sqrt{x} = x^{\frac{1}{2}}$

$\sqrt{x^2} = x^{2 *\frac{1}{2}} = x^{1}=x$

Es gilt auch: Die n-te Wurzel aus x ist die Umkehrfunktion zur n-ten Potenz.

Zurück zur Aufgabe von oben „Nach wie vielen Tagen ist G = 162?“ Oder anders gefragt: Für welches t gilt ?

$G(t) =162 = 2 * 3^{\frac{t}{6}}$

$162 = 2 * 3^{\frac{t}{6}} |:2$

$81 = 3^{\frac{t}{6}} |log_{3}$

$log_{3}{(81)} = \frac{t}{6}$

$4 = \frac{t}{6} | *6$

$24 = t$

Nach 24 Tagen ist die Größe 162.

Beim expontiellen Zerfall interessiert man sich auch oft für die Halbwertzeit. Bzw. der exponentielle Zerfall wird in Form der Halbwertzeit angegeben, wie beispielsweise bei radioaktiven Endprodukten wie Plutonium 239 und 240 der zivilen oder militärischen Nutzung der Kernspaltung von Uran-238. Bis heute wurden weltweit etwa Tausend Tonnen Plutonium erzeugt.

Das Isotop Plutonium 239 hat eine Halbwertzeit von 24.110 Jahren. Die Formel für den radioaktiven Zerfall ergibt sich zu:

$G(t) = G(0)* (\frac{1}{2})^{\frac{t}{24.110}}$

Von einem Anfangsbestand von G(0)=1 mg Plutonium 239 ist nach einem langen Menschenleben von 100 Jahren noch 0,997 mg übrig:

$G(100) = 1 * (\frac{1}{2})^{\frac{100}{24.110}} = 0,997$

Rechnen

Brutto Netto Umrechnung

Beitragsautor Von admin
Beitragsdatum Januar 7, 2021

Bereits im Kapitel Bruchrechung tauchte das Thema Prozentrechnung auf. Prozent heißt von Hundert. p Prozent (%) sind:

$p\% = \frac{p}{100}$

p % der Menge M ist die Teilmenge T

$T= \frac{p}{100} * M = \frac{p * M}{100}$

Von Brutto- und Nettobeträgen spricht man, wenn auf den Nettobetrag N eine Steuer S in Form eines festen Prozentsatzes p erhoben wird: S = N*p. Der Bruttobetrag B ist N+S:

$B = N * (1+p)$

Die Mehrwertsteuer, auch Umsatzsteuer genannt, wird vom Staat für alle gewerblich verkauften Waren erhoben. Sie beträgt im allgemeinen

$p=19\%=\frac{19}{100}=0,19$

Sie wird insbesondere auf allen Quittungen ausgewiesen. Das Verhältnis von Netto und Brutto ist daher der Faktor (1+p) = 1,19:

Der Kunde bezahlt den Bruttobetrag B=N*1,19,
der Verkäufer führt als Steuer s=N*0,19 ab und
behält als Einnahme den Nettoumsatz N.

Kleinstunternehmer bis 30.000 € Jahresumsatz sind umsatzsteuerbefreit. Gehörst du als Unternehmer nicht mehr dazu, dann musst du um beispielsweise 10 € netto einzunehmen, einen Brutto-Verkaufpreis von 10 € *1,19 = 11,90 € ausweisen.

Rechnen

Potenzfunktionen mit ganzzahligem Exponenten

Beitragsautor Von admin
Beitragsdatum Januar 7, 2021

Lineare Funktion (Gerade)

$f(x) = mx+b$

m ist die Steigung, d.h. der Wert, um den $f(x)$ steigt, wenn x um eins größer wird und
b ist der y-Achenabschnitt, also der Wert, den $f(x)$ an der Stelle $x=0$ annimmt, also $f(0)=b$

Beispiel:

$f(x) = 2x+3$

Um die Nullstelle x₀ einer Funktion zu ermitteln, muss die Funktion gleich Null gesetzt werden:

$0=f(x_0)$

$0=2x_0 + 3 | -3$

$-3=2 x_0 | :2$

$x_0 = -\frac{3}{2}$

Quadratische Funktion (Parabel)

$f(x) = ax^2+bx +c$

Die Parameter a, b, c nennt man die Koeffizienten der Potenzen

$x^2 , x^1 = x, x^0 = 1$

Beispiel:

$f(x) = 2x^2 - 12 x + 16$

Den Schnittpunkt mit der y-Achse liest man direkt ab, denn

$f(0) = 16$

Rechnung erfordert die Ermittlung der Nullstellen, von denen es 2, 1 oder 0 geben kann, je nachdem wie der Graph liegt und die Berechnung des Extremums, das je nach Orientung des Graphens ein Minimum oder Maximum ist.

Die Ermittlung der Nullstellen erfolgt in 3 Schritten:

Gleich Null setzen

$0 = 2x^2 - 12 x + 16$

Den Faktor vor dem x² -Term ausklammern

$0 = 2 (x^2 - 6x + 8) | : 2$

p/q-Formel anwenden für

$0 = x^2 - 6x + 8$

p/q-Formel

$0 = x^2 + p x + q$

$x = -\frac{p}{2} \pm \sqrt{(\frac{p}{2})^2 - q}$

Also sind: p=-6 und q= 8

$x = 3 \pm \sqrt{9-8}$

Die Nullstellen sind daher:

$x_1 = 4, x_2 = 2$

Die Extremstelle ist das arithmetische Mittel der Nullstellen

$x_E = \frac{2+4}{2}=3$

Da der Parameter des x² -Terms $>0$ ist, ist die Parabel nach oben geöffnet und der Extremwert ist ein Minimum.
Den Funktionswert des Minimums erhält man durch Einsetzen der Extremstelle x_E = 3:

$f(x_E) = 2x_E^2 - 12 x_E + 16 |x_E=3$

$f(3) = 2 *3^2 - 12 *3 + 16$

$f(3) = -2$

Das Minimum ist also

$S=(3|-2)$

Mit diesen Werten kann man die Parabel in die Scheitelpunktform bringen:

$f(x) = 2 (x-3)^2-2$

Und nur mit dem Wissen der Nullstellen kann man die Parabel in die Produktdarstellung bringen, aus der sich die Nullstellen 2 und 4 direkt ablesen lassen.

$f(x) = 2 (x-2)(x-4)$

Rechnen

Termumformung

Beitragsautor Von admin
Beitragsdatum Dezember 30, 2020

Regeln:

$a+b = b+a$

$a-b = a +(-b) = -b + a$

$a+ b + c = a + (b+c)$

$a*(b+c) = a*b + a*c$

$a*b = b*a$

$a:b = a *\frac{1}{b} = \frac{1}{b} * a = \frac{a}{b}$

Es gilt auch:

$(a+b)*(c+d) = a*c+a*d+b*c+b*d$

$\frac{a}{b} + \frac{a}{c} = a*(\frac{1}{b} + \frac{1}{c})$

$\frac{b}{a} + \frac{c}{a} = \frac{1}{a}*(b+c)$

Beispiel 1

$2x^2 +4x+ 2 = 2*(x^2+2x+1)$

$2x^3y +4x^2y+ 2xy$

$= 2xy (x^2+2x+1)$

Beispiel 2

Aus

$(a+b)(c+d) = ac+ad+bc+bd$

leiten sich die binomischen Formel ab:

$(a+b)^2 = a^2 + 2ab + b^2$

$(a-b)^2 = a^2 - 2ab + b^2$

$(a+b)(a-b) = a^2 - b^2$

Rechnen

Bruchrechnung

Beitragsautor Von admin
Beitragsdatum Dezember 30, 2020

Bruchrechnung

Regeln

$a:b=\frac{a}{b}$

$\frac{a}{b} + \frac{c}{b}= \frac{a+c}{b}$

$\frac{a}{b} * c= \frac{a*c}{b}$

$\frac{a}{b} * \frac{c}{d}= \frac{a*c}{b*d}$

$\frac{a}{b} : d= \frac{a}{b*d}$

$\frac{a}{b} : \frac{d}{c}= \frac{a}{b} * \frac{c}{d}= \frac{a*c}{b*d}$

Erweitern eines Bruches mit dem Faktor c:

$\frac{a}{b} = \frac{a * c}{b * c}$

Zur Addition von Brüchen muss man diese durch Erweitern auf einen gemeinsamen Nenner bringen:

$\frac{a}{b} + \frac{c}{d} = \frac{a*d}{b*d} + \frac{c*b}{d*b} = \frac{a*d + c*b}{b*d}$

Beispiel 1

Ist eine Teilmenge T ein Fünftel einer Menge M, dann ist

$T= \frac{1}{5} * M$

Ist die Menge M = 17, dann ist:

$T= \frac{1}{5} * 17 = \frac{17}{5}$

Der Taschenrechner sagt einem dann:

$\frac{17}{5} = 3,4$

Diese Kommazahlen nennt man auch Dezimalbruch. Dezimal heißt auf die Grundlage 10 bezogen:

$3,4 = \frac{34}{10}$

Gerne gibt man Teilmengen auch in Prozent an. Prozent heißt von Hundert. p Prozent (%) sind

$p\% = \frac{p}{100}$

p % der Menge M ist die Teilmenge

$T= \frac{p}{100} * M = \frac{p * M}{100}$

Z.B. sind 20% von 17

$T= \frac{20}{100} * 17 = \frac{17* 20}{100} = \frac{17* 20}{100}\ = \frac{340}{100}$

Und das ist nun wieder ein Dezimalbruch

$\frac{340}{100}=\frac{34}{10}=3,4$

Es gilt also:

$20\%= \frac{1}{5}$

Das erklärt sich dadurch, dass

$20\%= \frac{20}{100}$

und dieser Bruch gekürzt werden kann, d.h.

$\frac{20}{100} = \frac{1}{5}$

Beispiel 2:

Gegeben seien die Teilmengen T₁ und T₂

$T_1=\frac{1}{5}, T_2=\frac{1}{4}$

Die Summe der Teilmengen ist dann:

$T_1 + T_2 = \frac{1}{5} + \frac{1}{4} = \frac{1*4}{5*4} + \frac{1*5}{4*5} = \frac{4}{20} + \frac{5}{20} = \frac{9}{20}$

Rechnen

Potenzen

Beitragsautor Von admin
Beitragsdatum Dezember 30, 2020

Regeln

$x^0=1$

$x^1=1$

$x^{n+m} = x^n * x^m$

$x^{-m}= \frac{1}{x^m}$

$\sqrt[m]{x} = }x^{\frac{1}{m}$

$( x^n)^m = x^{n*m}$

Daraus leitet sich ab:

$x^{n-m} = \frac{x^n}{x^m}$

$\sqrt[m]{x^n} = }x^{\frac{n}{m}$

Es gilt:

$(xy)^n = (x*y)^n = x^n * y^n = x^n y^n$

$\sqrt[n]{xy}=\sqrt[n]{x*y} =$

$\sqrt[n]{x} * \sqrt[n]{y} = \sqrt[n]{x} \sqrt[n]{y}$

Aber niemals niemals nie können Potenzen und Wurzeln in Summen reingezogen werden:

$(x+y)^n \neq x^n + y^n$

Z.B. ist

$(x+y)^2 = x^2 + 2xy + y^2 \neq x^2 + y^2$